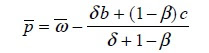A Oferta Agregada: Um Exemplo Algébrico - II

Tweet

O contrato de trabalho estipula o salário nominal no início do período, todavia o nível de emprego será variável de acordo com o nível de preços que efetivamente ocorrer no período, pois a contratação ou dispensa de trabalhadores será feita de acordo com a equação de demanda de mão-de-obra. Substituindo-se a quantidade de mão-de-obra dada pela equação de demanda de mão-de-obra,

O nível de produção responde positivamente a aumentos do nível de preços e negativamente a acréscimos no salário nominal. Substituindo-se o valor do salário nominal, ω , na expressão anterior obtém-se a equação da curva de oferta agregada:

A Oferta Agregada: Um Exemplo Algébrico - I

Tweet Suponha que o nível de produção e a quantidade de mão-de-obra estão ligados através da seguinte função de produção,

Neste modelo os contratos de trabalho especificarão o salário nominal de cada trabalhador no início do período de produção, de sorte a igualar a oferta e a demanda de mão-de-obra, levando-se em conta o nível de preços esperado ao final do período. Denominando-se por ω o salário nominal que equilibraria o mercado de trabalho se o nível de preços for igual ao previsto, temos das equações de demanda e oferta de mão-deobra:

Modelo de Gray-Fischer - IV

Tweet Não seria difícil verificar-se que para cada nível de preços esperado corresponderia uma curva de oferta agregada no curto prazo. A Figura 17 ilustra esta proposição. Quando o nível de preços antecipado é igual a Po e, a curva de oferta é dada por S Po ( e ) .

Figura 17. Curvas de Oferta Agregada Para Diferentes Índices de Preços Esperados

Modelo de Gray-Fischer - III

Tweet

Quando o nível de preços antecipado for igual ao observado, o volume de emprego será igual a N e o nível de produção será igual a y , como ilustrado na Figura 16. Se o nível de preços for maior do que aquele que era esperado (Po > Pe), o volume de emprego será superior ao nível de pleno emprego ( N N ) 0 > , e o nível de produção também o será, isto é, y y 0 > . Por outro lado, quando o nível de preços for inferior ao que era esperado (P1 < Pe), haverá uma redução no nível de emprego e uma conseqüente diminuição da produção na economia. Portanto, a curva S(Pe) indica os níveis de preços e de renda real de equilíbrio, no curto prazo, para cada nível de preços esperado.

Figura 16. A Curva de Oferta Agregada: Curto x Longo Prazo

Modelo de Gray-Fischer - II

Tweet O salário nominal é medido no eixo vertical e o volume de emprego no eixo horizontal. As curvas de demanda e de oferta de mão-de-obra são traçadas para o mesmo nível de preços esperado (Pe). Na interseção das duas curvas, a quantidade demandada é igual à ofertada (Nd = Ns). O salário nominal é igual, então, a W e o nível de pleno emprego é igual a N . Uma vez fixado o salário nominal, o nível de emprego efetivo dependerá do nível de preços observado. Com efeito, suponha que o nível de preços atual (Po) seja aquele que era esperado (Po > Pe). A curva de demanda de mão-de-obra, na Figura 15, desloca-se para cima porque agora os empresários estão dispostos a pagarem maiores salários, para cada nível de emprego, em virtude do aumento dos preços. Como o salário nominal está fixo, o volume de emprego será igual a No, que é superior ao nível considerado de pleno emprego. Obviamente, esta situação é transitória, porque os trabalhadores estão momentaneamente fora de suas curvas de oferta de longo prazo. Na hipótese de que o nível de preços seja inferior àquele que era antecipado (P1 < Pe), a curva de demanda desloca-se para baixo porque os empresários estariam dispostos a pagarem salários nominais menores em virtude da queda do nível de preços em relação àquele que era esperado. Em conseqüência, eles ajustam o nível de emprego através de demissões, diminuindo o número de homens-hora para N1.

Figura 15. A Determinação do Nível de Emprego

Modelo de Gray-Fischer - I

Tweet

O modelo de Gray-Fischer supõe que o mercado de mão-de-obra funciona do seguinte modo. No início de cada período, com base no nível de preços que é antecipado pelos trabalhadores e empresários, os salários nominais são determinados de sorte a equilibrar a oferta e a procura de mão-de-obra. Os salários nominais permanecem fixos durante todo o período de vigência do contrato de trabalho, e os empresários são livres para contratarem e despedirem trabalhadores durante o período de vigência do contrato. Neste modelo, portanto, não existe a assimetria de informação do modelo friedmaniano, pois o salário nominal é determinado com base na expectativa de preços dos trabalhadores e dos empresários. Como no modelo keynesiano, o modelo de Gray-Fischer admite que no curto prazo, o salário nominal é rígido e que o mercado de mão-de-obra pode estar em desequilíbrio. No longo prazo, como no modelo neoclássico, os salários e preços são flexíveis de sorte a equilibrar o mercado de trabalho. A Figura 14 ilustra o funcionamento do mercado de trabalho. 

Figura 14.A Determinação do Salário Nominal

Modelo de Friedman - III

Tweet Exemplo Algébrico Considere-se o modelo formado pelas seguintes equações:

A equação de oferta de mão-de-obra depende do logaritmo do nível de preços esperado (pe). As demais equações são idênticas às equações do modelo neoclássico. O mercado de trabalho está sempre em equilíbrio. No curto prazo o nível de preços pode divergir do preço antecipado pelos trabalhadores. O equilíbrio de longo prazo requer que as previsões dos trabalhadores se materializem. As três últimas equações do modelo quando resolvidas fornecem a seguinte expressão para o volume de emprego da economia:

onde n = b − c δ +1−β é o nível de pleno emprego. Quando p > pe, segue-se que n > n e se p < pe n < n . Substituindo-se este valor de n na função de produção, obtém-se a seguinte equação de oferta agregada:

que é a Curva de Phillips do modelo friedmaniano.

Figura 12. A Oferta Agregada Figura 13. A Curva de Phillips

Modelo de Friedman - II

Tweet Nestas circunstâncias, existe equilíbrio tanto no curto como no longo prazo, pois ambos os lados do mercado estão nas suas posições preferidas, Quando os trabalhadores antecipam um nível de preços menor do que aquele que efetivamente ocorre, eles oferecem um volume de mão-de-obra acima do nível de pleno emprego, pois esperavam um salário real elevado que na verdade não se materializou. Esta situação não é de equilíbrio de longo prazo, porque os trabalhadores acabarão por reconhecer que tomaram uma decisão errada, e irão rever o volume de emprego que desejam oferecer diante das novas condições da economia. Quando os trabalhadores antecipam um nível de preços superior ao que ocorreu, o volume de emprego é inferior ao de pleno emprego e suas decisões serão revistas face ao erro de previsão. No modelo de Friedman os níveis de emprego e de produto real variam, no curto prazo, em virtude dos erros de previsão dos trabalhadores. Para um dado nível de preços esperado ( Pe ) 0 , quanto maior o nível de preços (P) maior será o produto real da economia. Quando o nível de preços for igual ao valor antecipado pelos trabalhadores ( P = Pe ) 0 , o produto real será igual ao produto de pleno emprego. A Figura 11 mostra as curvas de oferta agregada de curto prazo, que são positivamente inclinadas, e a curva de oferta agregada de longo prazo que é vertical, como no modelo neoclássico.

Figura 11. A Oferta Agregada: Modelo Friedmaniano

Modelo de Friedman - I

Tweet O modelo do mercado de trabalho apresentado por Friedamn, em seu discurso presidencial da Associação de Economistas Americanos, admite como hipótese básica uma assimetria no conjunto de informações dos trabalhadores e dos empregadores: os trabalhadores oferecem sua força de trabalho com base no nível de preços esperado, enquanto os empregadores contratam a mão-de-obra conhecendo de antemão os preços dos bens que irão produzir. As equações do mercado de trabalho, são, então, dadas por:

O nível de preços esperado Pe é exógeno, e no momento não nos interessa o mecanismo pelo qual os trabalhadores formam suas expectativas sobre o futuro. Graficamente a Figura 10 descreve o funcionamento do mercado de trabalho. Quando os trabalhadores acertam nas suas expectativas, Pe = P, o volume de emprego é igual a N .

Figura 10. Mercado de Trabalho: Hipótese Friedmaniana

Exemplo Algébrico - II

Tweet Quando o salário real é superior ao de pleno emprego, o volume de emprego é dado pela curva de demanda de mão-de-obra. Substituindo-se o valor de nd na função de produção obtém-se a curva de oferta agregada da economia:

A Figura 9 mostra a curva de oferta agregada deste exemplo. Até o nível de preços

a curva de oferta agregada é positivamente inclinada. A partir daí ela é vertical

Figura 9. A Curva de Oferta Agregada do Modelo Log-Linear: Salário Nominal Rígido

Exemplo Algébrico - I

Tweet Tomemos o mesmo exemplo algébrico da seção anterior, com a introdução da hipótese da rigidez de salário nominal e, portanto, de desequilíbrio no mercado de trabalho. As equações do modelo são as seguintes:

Admitiremos que o salário nominal ω é tal que, ao nível de preços p, o salário real é maior do que aquele que prevaleceria na situação de pleno emprego, ou seja:

Na hipótese oposta, quando o salário ω fosse tal que o salário real estivesse abaixo do salário real de pleno emprego, haveria excesso de demanda de mão-de-obra. Este excesso de demanda elevaria os salários nominais pois, por hipótese, eles não são rígidos para cima. Esta hipótese pode, portanto, ser descartada por não apresentar nenhum interesse prático.

Modelo Keynesiano - II

Tweet Se o nível de preços aumentasse de Po para P1, o salário real cairia, e o nível de emprego aumentaria. Portanto, para um dado salário nominal, quando o nível de preços cresce, o nível de emprego, e consequentemente o produto real também cresce, até atingir o nível de pleno emprego e do produto potencial da economia. A curva de oferta agregada da economia é positivamente inclinada até o nível de preços P1, onde ela se torna vertical como indicado na Figura 8.

Figura 8. Oferta Agregada: A Hipótese Keynesiana de Salário Rígido

Modelo Keynesiano - I

Tweet O modelo keynesiano pressupõe que o salário nominal é rígido para baixo, pois o salário é maior ou quando muito igual a W . Isto é:

A Figura 7 mostra o funcionamento do mercado de trabalho na hipótese keynesiana de salário rígido. Quando o salário nominal é igual a W , a quantidade demandada de mão-de-obra, ao nível de preços Po, é igual a No, como indicado na Figura 7. Nestas circunstâncias o salário real está acima daquele nível que equilibra o mercado de trabalho. Como o salário nominal não pode diminuir, o volume de emprego (No) ficará aquém do nível de pleno emprego ( N ) .

a) Salário Real x Volume de Emprego     b) Salário Nominal x Volume de Emprego

Figura 7. Mercado de Trabalho: Salário Nominal Rígido

Exemplo Algébrico

Tweet Suponha que a função de produção seja expressa por:

onde y e n são, respectivamente, os logaritmos do produto real e do volume de emprego. A igualdade entre o salário real e a produtividade marginal do trabalho fornece a seguinte equação de demanda de mão-de-obra:

onde b = a + log β e ω e p são, respectivamente, os logaritmos do salário nominal e do nível de preços. A equação de oferta de mão-de-obra é dada por:

O mercado de trabalho estará em equilíbrio quando:

As quatro equações anteriores fornecem os seguintes valores para o nível de produto, o volume de emprego e o salário real na situação de equilíbrio:

Modelo Neoclássico - VI

Tweet De acordo com a função de produção, a este nível de emprego corresponde um produto igual a y = f ( N ,K ). A curva de oferta agregada, com nível de preços marcado no eixo vertical e com o nível do produto real no eixo horizontal, é vertical no modelo neoclássico.
A economia estaria sempre em pleno emprego em virtude da flexibilidade de preços e de salários

Figura 6. Modelo Neoclássico: Oferta Agregada Vertical

Modelo Neoclássico - V

Tweet

Figura 5. Efeito de Mudança de Preços Sobre o Salário Nominal

o mesmo nível de emprego N, e o mesmo salário real W1/P1 = Wo/Po, como indicado na Figura 5. Portanto, para qualquer nível de preços o volume de emprego é constante e igual a N .

Modelo Neoclássico - IV

Tweet O modelo neoclássico supõe que os salários e preços são flexíveis, de tal sorte que o mercado de mão-de-obra está sempre em equilíbrio, com a quantidade demandada igual à ofertada:

A Figura 4 mostra o equilíbrio do mercado de mão-de-obra. O volume de emprego é igual a N. O salário real é igual a Wo/Po e o salário nominal é Wo. Quando o nível de preços se altera, as curvas de demanda e oferta no plano W e N deslocam-se de tal sorte a manter

a) Determinação do Salário Real                     b) Determinação do Salário Nominal

Figura 4. Modelo Neoclássico: Equilíbrio do Mercado de Mão-de-Obra

Modelo Neoclássico - III

Tweet negativamente inclinada. Na Figura 2b o eixo vertical mede o salário nominal. Neste caso, a curva de demanda depende do nível de preços. Assim, para o nível de preços P1, a curva de demanda D(P1) está acima dos pontos correspondentes à curva D(Po), pois P1 é maior que Po.
 Admita-se que a quantidade de mão-de-obra ofertada depende do salário real do indivíduo, e que essas duas variáveis estão positivamente correlacionadas. Isto é:

Na Figura 3a representa-se esta equação pela curva SS. No eixo vertical mede-se o salário real e no eixo horizontal o volume de emprego. A curva é positivamente inclinada, pois supõe-se que o salário real e o nível de emprego movem-se na mesma direção pelo lado da oferta. Na Figura 3b o eixo vertical mede o salário nominal. Agora, para cada nível de preços corresponde uma curva de oferta.. Assim, para o volume de emprego igual a No, o salário nominal desejado pelos trabalhadores é igual a Wo quando o nível de preços é Po, e igual a W1 quando o nível de preços é P1.

a) Salário Real x Emprego           b) Salário Nominal x Emprego

Figura 3. A Oferta de Mão-de-Obra

Modelo Neoclássico - II

Tweet

Figura 1.A Função de Produção onde g N f N ( d ) = (N,K). ∂ ∂ Como a produtividade marginal da mão-de-obra decresce com o aumento de sua quantidade, segue-se que a curva de demanda de mão-de-obra, na Figura 2a, é

a) Salário Real x Emprego                b) Salário Nominal x Emprego

Figura 2. A Demanda de Mão-de-Obra

Modelo Neoclássico - I

Tweet O nível de produção é função do volume de mão-de-obra empregada e do estoque de capital existente na economia, de acordo com a seguinte função de produção:

Supõe-se que, no curto prazo, o estoque de capital é constante, daí K = K . A produtividade marginal da mão-de-obra é positiva (fN = ∂f/∂N > 0) e ela decresce quando a quantidade de mão-de-obra aumenta, isto é: fNN = ∂2 f/∂N2 < 0. A Figura 1 mostra a função de produção para um dado estoque de capital. No eixo vertical mede-se o nível de produção e no eixo horizontal a quantidade de mão-de-obra. A tangente num ponto da curva, como no ponto
A, por exemplo, é igual a produtividade marginal da mão-de-obra. Acréscimos no estoque de capital deslocam a curva OAB para cima e para a esquerda. Uma empresa competitiva que tem como objetivo maximizar o lucro, demandará uma quantidade de mão-de-obra tal que a produtividade marginal da mesma seja igual ao salário real, isto é:

A OFERTA AGREGADA

Tweet

A oferta agregada no modelo de curto prazo, pode ser desenvolvida a partir de diferentes concepções do funcionamento do mercado de mão-de-obra, da fixação de preços pelas empresas, de diferentes hipóteses quanto à flexibilidade do sistema de preços na economia e quanto aos mecanismos de formação de expectativas dos agentes econômicos. 

Em alguns modelos supõe-se mercados competitivos onde as empresas são tomadoras de preços (price takers), com preços iguais aos custos marginais de produção, em outros modelos admite-se que as empresas determinam seus preços adicionando-se ao custo unitário de produção, uma certa margem (as empresas são, nestas circunstâncias, price makers). 

Em vários modelos, admite-se que existe, pelo menos no curto prazo, rigidez nos salários, rigidez esta que é responsável pela existência de desemprego na economia. Nos modelos que serão apresentados a seguir, deduz-se uma correlação positiva, no curto prazo, entre o nível de preços e o nível de renda real, ou entre a taxa de inflação e a renda real. No longo prazo, o nível de preços ( ou a taxa de inflação) independe do nível de renda real da economia. No curto prazo, o modelo apresenta propriedades keynesianas com ajustes nas quantidades e nos preços. No longo prazo, o modelo torna-se neoclássico, pois todos os ajustes são nos preços.

A Determinação dos Preços Num Modelo Neoclássico com Expectativas Racionais - VII

Tweet De acordo com a equação de demanda agregada, o nível de preços da economia será igual a:

Substituindo-se as demais equações do modelo na expressão acima, e levando-se em conta a solução adotada para o nível de preços esperado, chega-se ao seguinte resultado:

O nível de preços observado tem dois componentes. O componente antecipado depende das políticas monetária, fiscal e do nível do produto de pleno emprego. O segundo componente, que é a parte não antecipada, depende dos choques que ocorrem no sistema, sejam de política ou de comportamento dos agentes econômicos.

A Determinação dos Preços Num Modelo Neoclássico com Expectativas Racionais - VI

Tweet O ponto E da Figura 38 é o ponto de equilíbrio do modelo, apesar dele ser instável. Quando ocorre uma mudança antecipada na política monetária, ou na política fiscal, ou no nível de produto potencial, o nível de preços ajusta-se instantaneamente, passando, digamos, do ponto E1 para o ponto E2, como indicado na Figura 39.

Figura 39. Mudanças Antecipadas no Equilíbrio

A hipótese de que o nível de preços esperado permanecerá constante no futuro apesar de bastante plausível, eliminando-se a possibilidade do aumento dos preços por um processo de combustão espontânea, é casuística, pois não está fundamentada no comportamento dos agentes econômicos.

A Determinação dos Preços Num Modelo Neoclássico com Expectativas Racionais - V

Tweet A literatura sobre modelos com expectativas racionais tem apresentado uma série de hipóteses adicionais para restringir o conjunto de soluções do modelo. Uma dessas hipóteses é de que a partir de uma certa data futura o nível de preços esperado se estabiliza:

Substituindo-se a solução da equ

ação de diferenças finitas nesta condição, obtémse Simplificando-se resulta:

Como α = 0, esta restrição só é satisfeita se:

Isto é, se acredita que os preços irão se estabilizar no futuro, eles se estabilizam hoje, e, portanto, para qualquer período tem-se:

A Determinação dos Preços Num Modelo Neoclássico com Expectativas Racionais - IV

Tweet

Uma das características importantes desse modelo é de que ele não fornece o valor esperado inicial pt e para o nível de preços. 

Para qualquer valor que se arbitre para pt e temse uma solução de equação de diferenças finitas. Colocando-se a mesma questão de outro modo: qualquer valor previsto para o futuro é consistente com algum valor para pt e . 

Consequentemente, o modelo apresenta uma infinidade de soluções. Outra propriedade importante desse modelo é de que se pt e for diferente de θ /α ( p θ /α ) t e = , o nível de preços cresce indefinidamente, como se pode verificar no diagrama de fases da Figura 38. O modelo produz uma "bolha"(bubble) para o nível de preços, pois os preços subiriam por combustão espontânea, simplesmente pelo fato de se prever que eles subiriam.

Figura 38. Diagrama de Fases

A Determinação dos Preços Num Modelo Neoclássico com Expectativas Racionais - III

Tweet

A segunda equação nos diz que o nível do produto flutua randomicamente em torno do nível de pleno emprego ( y ), de acordo com a variável aleatória ut. 

As duas últimas equações representam as políticas fiscal e monetária que têm como objetivo atingirem, na média, os valores f em. As variáveis vt e η t são variáveis aleatórias, e como as demais εt e ut, têm médias zero, variâncias constantes, não são correlacionadas serialmente e são ortogonais entre si. 

A hipótese de expectativa racionais eqüivale a dizer que o valor esperado do nível de preços é igual à esperança matemática do mesmo, da distribuição condicionada pela informação disponível no período t-1. Isto é:

No que se segue simplificaremos a notação representando a variável t-1 pt e +1 por pt e +1, suprimindo o índice t-1, pois neste exemplo as esperanças matemáticas são computadas no período t-1. Tomando-se a esperança matemática de ambos os lados da equação de demanda agregada e levando-se em conta que as esperanças matemáticas de yt , f e m, são respectivamente, iguais a y , f e n , obtém-se o seguinte resultado:

onde θ = − y + k + α m + γ f . Esta equação é uma equação linear de diferenças finitas de primeira ordem, cuja solução é dada por: